- Главная
- Велоспорт
- Тренировка
- 1984 год
- Анализ тактики в индивидуальной гонке преследования на 4 км
Анализ тактики в индивидуальной гонке преследования на 4 км
Дата: Январь 1984
Тактика прохождения дистанции в индивидуальной гонке преследовании на 4 км заключается в умении спортсмена рационально распределить усилия на дистанции в зависимости от типа заезда, когда необходимо либо показать высокий результат, либо добиться победы над соперником (Красников А. А., 1966, Бахвалов В. А., 1979). При этом спортсмены должны учитывать внешние и внутренние факторы, влияющие на спортивный результат: качество экипировки, инвентаря и полотна трека, метеоусловия (если трек открытый) и др. Из внутренних факторов наибольшее значение имеют уровень специальной подготовленности спортсменов на данном этапе и индивидуальные особенности механизмов энергообеспечения, влияющие на тактические варианты прохождения дистанции.
В результате типологии раскладок соревновательной скорости в индивидуальной гонке преследования на 4 км было предложено несколько различных вариантов динамики дистанционной скорости. Так, В. А. Бахвалов (1966) выделил пять различных вариантов раскладки, а А. А. Красников (1968) рекомендовал рассматривать только три варианта. Ю. К. Дравниек (1981), проанализировав более 1000 заездов на этой дистанции, выделил четыре варианта. Практически вс-е авторы, изучающие типологию раскладок, как правило, выделяют четыре основных типа распределения усилий на дистанции:
Большинство авторов считают, что наиболее рациональным вариантом распределения усилий в индивидуальной гонка преследования на 4 км является относительно равномерное поддержание скорости на всей дистанции (1-й тип). Критерием оптимальности тактики при этом, как правило, выбирается сам спортивный результат (Т — →min) и реже среднее линейное отклонение скорости на отдельных участках дистанции от среднедистанционной скорости в гонке
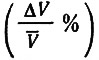
Некоторые авторы, например Ю. К. Дравниек (1977—1981) и М. А. Андрюнин с соавт. (1981) основным критерием оптимальности тактики считают показатель энергетической стоимости выполненной работы. Ими было определено, что тактические варианты распределения сил индивидуально-оптимальны и зависят от энергетического потенциала спортсмена.
Итак, на сегодняшний день у специалистов по велосипедному спорту нег единого мнения по вопросу выбора оптимальной тактики в индивидуальной гонке преследования на 4 км. В связи с этим целью нашего исследования явилось изучение закономерностей тактики в условиях соревновательной деятельности гонщиков-преследователей.
Для этого в работе были поставлены следующие задачи:
1. Определить тактические варианты прохождения дистанции индивидуальной гонки преследования на 4 км спортсменами высокой квалификации.
2. Выявить особенности тактики прохождения дистанции 4 км в зависимости от типа заезда.
Вся работа была проведена на олимпийском велотреке в Крылатском, позволяющем более качественно изучить тактическую деятельность велосипедистов, поскольку на варианты распределения усилий в гонке не оказывают влияния метеоусловия и другие факторы, имеющие место на открытых треках.
Было проанализировано более 150 графиков прохождения дистанции индивидуальной гонки преследования на 4 км сильнейшими гонщиками СССР и мира за период с 1980 по 1983 г. На первом этапе работы было рассмотрено 80 графиков предварительных заездов, в которых спортсмены отбираются в числе 16 или 8 участников, продолжающих борьбу в соревнованиях. По мнению ряда авторов (В. А. Бахвалов, 1960; А. А. Красников, 1968, Ю. Г. Крылатых, 1980 и др.), именно в заездах на время велосипедисты стремятся пройти дистанцию с оптимальной скоростью, а вариант распределения усилий на дистанции отражает уровень их специальной подготовленности.
На втором этапе работы исследовалась динамика скорости преодоления дистанции 4 км в финальных заездах.
Анализ графиков прохождения гонщиками дистанции в индивидуальной гонке преследования на 4 км показал, что на различных участках дистанции изменяется:
Однако информация, полученная при регистрации и анализе динамики соревновательной скорости, сама со себе не позволяет решить вопрос о причинах изменения скорости на дистанции. Иными словами, не ясно, приводит ли увеличение скорости на предыдущем участке дистанции к вынужденному снижению скорости на последующем, более ясную картину дает корреляционный анализ связей между величинами скорости на отдельных километрах дистанции гонки. Заметим, что использовать корреляционный анализ можно лишь в том случае, если результаты измерения подчиняются закону нормального распределения.
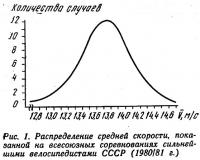
Поэтому был построен график эмпирического закона распределения средней скорости в исследуемых заездах (рис. 1). В результате было установлено, что средние величины скорости велосипедистов подчиняются нормальному закону распределения. Поэтому для вычисления коэффициентов корреляции можно использовать формулу Бравэ-Пирсона (табл. 1).
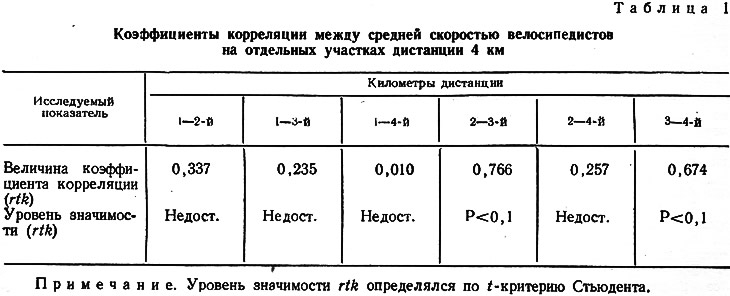
Из табл. 1 видно, что средняя скорость первого километра дистанции имеет незначительную связь со вторым километром и практически не оказывает влияния на третий и четвертый километры дистанции. А поддержание высокой скорости на втором километре положительно влияет на результат прохождения третьего километра дистанции (rtk=0,766). Способность удерживать высокую скорость на третьем километре дистанции положительно влияет на время преодоления четвертого километра (rtk=0,674). Следовательно, на среднюю скорость преодоления последующего участка дистанции оказывает влияние скорость, показанная на предыдущем участке.
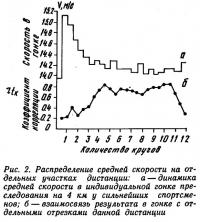
Статистические методы исследования позволили не только выявить влияние скорости прохождения одного участка дистанции на другой, но и определить значимость времени прохождения каждого участка дистанции на конечный результат. Для этого мы определили коэффициент корреляции между средней скоростью, показанной в гонке, и скоростью, зафиксированной на отдельных участках дистанции (рис. 2). Как видно, скорость на первых трех кругах имеет невысокую корреляционную связь с результатом в гонке (rtk=0,212—0,433). Средняя скорость, показанная с четвертого по одиннадцатый круги, имеет наибольшую корреляционную связь с результатом (rtk=0,613—0,844). Скорость на последних двух кругах имеет корреляционную связь с результатом на уровне rtk=0,251—0,655. Полученные данные свидетельствуют, что на результат в индивидуальной гонке преследования на 4 км оказывает влияние в основном способность гонщиков поддерживать высокую скорость в середине дистанции. Начало дистанции и финишное ускорение не являются определяющими в общем результате, поскольку выполняются всеми гонщиками с различной скоростью.
С этих позиций мы и подошли к изучению тактики в индивидуальной гонке преследования на 4 км у спортсменов высокой квалификации. В зависимости от динамики стартового ускорения, динамики скорости в середине и конце дистанции все исследуемые графики прохождения дистанции были разделены на 9 групп, представляющих различные варианты распределения усилий (табл. 2).
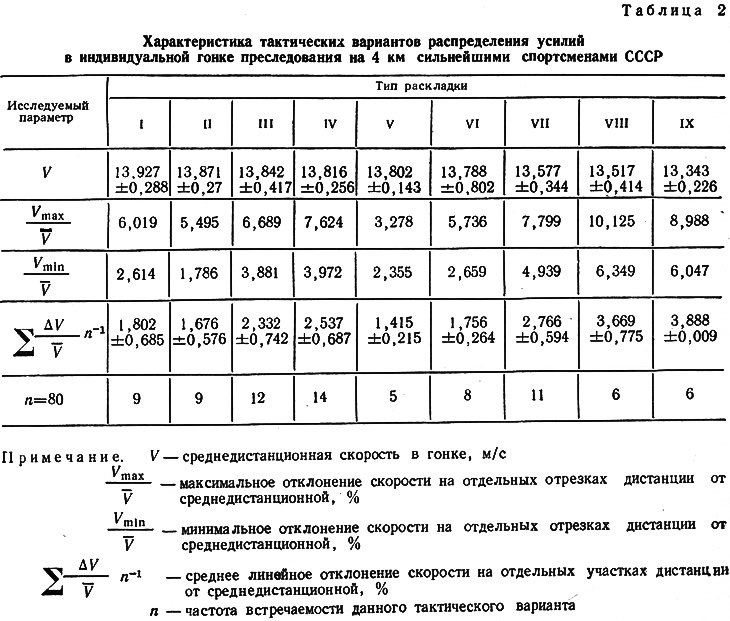
Поскольку ранее ни одна из классификаций динамики соревновательной скорости в гонке на 4 км не имела такого количества исследуемых тактических вариантов раскладок, мы предприняли попытку описать и охарактеризовать каждый из них.
1. Динамика дистанционной скорости носит переменный характер. После выполнения стартового ускорения и снижения скорости до уровня среднедистанционной наблюдается увеличение скорости в середине дистанции и ка финише при максимальном повышении скорости на старте +6,019% и снижении ее до —2,614%.
2. Скорость в начале дистанции превышает среднедистанционную на +9,495%, затем снижается (—1,726%) и остается практически неизменной до финиша.
3. Повышение скорости связано с выполнением сильного стартового ускорения, превышающего на 6,688% среднедистанционную скорость. В дальнейшем наблюдается снижение скорости сначала до уровня среднедистанционной, а затем и ниже среднедистанционной при максимальном снижении на —3,881% и некотором увеличении при финишном ускорении.
4. Разновидность третьего варианта при еще более сильном повышении скорости в начале дистанции (+7,624%) и характерном удержании скорости после каждого ее снижения. Максимальное снижение скорости составляет —3,972% от среднедистакционной.
5. Отмечается относительно равномерное прохождение дистанции. Максимальное повышение среднедистанционной скорости на старте составило +3,278%, а максимальное снижение в конце дистанции —2,355%.
6. Повышается среднедкстанционная скорость в начале и в конце дистанции и удерживается практически на одном уровне ниже среднедистанционной, в середине гонки. Максимальное повышение среднедистанционной скорости на старте составляет +5,736%.
7. Разновидность пятого варианта при значительном повышении среднедистанционной скорости на старте (+7,799%) и более раннем снижении скорости к финишу. Максимальное снижение среднедистанционной скорости составляет —4,939%.
8. Постепенное снижение скорости до финиша после выполнения стартового ускорения. Максимальное повышение среднедистанционной скорости составляет +10,125%, а минимальное снижение —6,349%.
9. После стартового ускорения скорость в гонке постепенно снижается практически на всей дистанции, за исключением короткого финишного отрезка, где скорость увеличивается. Максимальное повышение скорости составляет +8,988%, максимальное снижение —6,047% от среднедистанционной.
Рассчитанный коэффициент корреляции (rtk) меж_ду среднедистанционной скоростью в гонке (V) и величиной среднего линейного отклонения скорости на отдельных участках дистанции
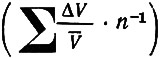
равен —0,790%, при P<0,1. Это свидетельствует, что высококвалифицированные велосипедисты стремятся к более равномерному поддержанию скорости на дистанции гонки. Явление это не случайное, а закономерное и зависит от индивидуальных возможностей организма спортсмена. Полученные данные по характеру динамики скорости в гонке согласуются с проведенными ранее лабораторными исследованиями при моделировании соревновательной деятельности на велоэргометре (А. И. Головачев, Ю. Г. Крылатых, 1981).
Чаще всего использовались варианты III, IV и VII, при которых среднедистанционная скорость наблюдалась в диапазоне 13,577—-13,842 м/с (см. табл. 2). Победители соревнований в основном применяли I и III тактические варианты, а аутсайдеры — V, VI, VIII и IX варианты.
Дальнейшее исследование тактики прохождения дистанции в индивидуальной гонке преследования на 4 км выявило, что на динамику скорости не всегда оказывают влияние действия соперника в заезде. Так, в различных по типу заездах было отмечено, что сильнейшие спортсмены мира стремятся придерживаться одного тактического варианта (рис. 3). Например, спортсмен из команды ГДР X. Вольф, занявший 4-е место на XXII Олимпийских играх, в предварительном, четвертьфинальном и полуфинальном заездах (см. рис. 3, а) преодолевал дистанцию, используя по предложенной нами классификации VIII тактический вариант. При этом в предварительном заезде, когда спортсмены стартовали по одному, X. Вольф установил новый мировой рекорд (4.39,96) для закрытых велотреков. В финальном заезде X. Вольф использовал VI тактический вариант, начав гонку медленнее, чем обычно на —2,25%. Относительно равномерно прошел 2-й и 3-й км дистанции и увеличил скорость на финише на +1,66% относительно среднеднстанционной. В этом заезде гонщик из ГДР показал один из лучших своих результатов (4.37,38), однако этого было недостаточно для победы над Х.-Х. Орстедом, занявшим 3-е место, — 4.36,54.
Чемпион Олимпийских игр 1980 года Р. Дилл-Бунди использовал в своих заездах VI тактический вариант (см. рис. 3, б). Учитывая свои скоростные возможности, швейцарский велосипедист начал гонку с высокой скоростью, превышая среднедистанционную более чем на 2—3%. Затем, после падения скорости на 1—2% ниже среднедистанционной, удерживал ее до девятого круга. В заключительной части дистанции, как правило, значительно увеличивал скорость (финишное ускорение), что позволило ему в финальном заезде на 8% превысить среднедистанционную скорость. Следует отметить, что при таком варианте распределения сил в гонке Р. Дилл-Бунди показал абсолютно лучшее время прохождения 4-километровой дистанции (4.32,29).
Таким образом, высокий спортивный результат в индивидуальной гонке преследования на 4 км может быть показан практически при любом варианте распределения усилий в гонке. Это еще раз подтвердило наше экспериментальное исследование в лабораторных условиях (М. А. Андрюнин с соавт., 1981), показавшее целесообразность использования понятия индивидуально-оптимального варианта распределения сил в гонке, позволяющего полностью исчерпать энергетический потенциал, зависящий от специальной подготовленности спортсменов. Поэтому мы считаем, что для каждого спортсмена существует свой индивидуально-оптимальный тактический вариант.
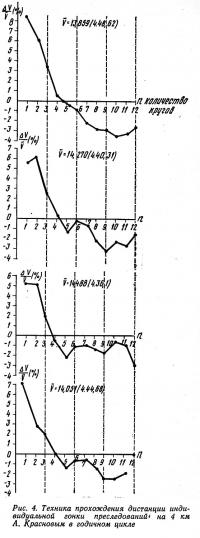
Отметим, что проводимое нами наблюдение за использованием вариантов распределения усилий в гонке сильнейшими велосипедистами СССР, выявило сохранение индивидуальных особенностей показателей тактики. Так, например, у неоднократного чемпиона СССР змс А. Краснова характер распределения усилий в гонках на протяжении 1980—1981 гг. (рис. 4) носил идентичный характер. Спортсмен использовал III тактический вариант. После превышения среднедистанционной скорости на 6— 8% во время стартового ускорения следовало снижение скорости до 5-го круга. Затем спортсмен удерживал скорость, близкую к среднедистанционной. Лучше всего А. Краснову удалось это сделать на зимнем первенстве СССР (27.01,81), где он показал высокий спортивный результат — 4.36,10.
Таким образом, мы пришли к выводу, что у велосипедистов высокой квалификации характер распределения усилий в гонке (динамика скорости) индивидуально-оптимален и сохраняется не только в зависимости от типа заезда, но и практически не изменяется на протяжении длительного времени участия в соревнованиях.
А. И. Головачев, ВНИИФК, Ю. Г. Крылатых, кандидат педагогических наук, ГЦОЛИФК.
В результате типологии раскладок соревновательной скорости в индивидуальной гонке преследования на 4 км было предложено несколько различных вариантов динамики дистанционной скорости. Так, В. А. Бахвалов (1966) выделил пять различных вариантов раскладки, а А. А. Красников (1968) рекомендовал рассматривать только три варианта. Ю. К. Дравниек (1981), проанализировав более 1000 заездов на этой дистанции, выделил четыре варианта. Практически вс-е авторы, изучающие типологию раскладок, как правило, выделяют четыре основных типа распределения усилий на дистанции:
- 1. Относительно равномерное прохождение дистанции.
- 2. Преодоление первой половины дистанции быстрее, чем второй.
- 3. Преодоление второй части дистанции быстрее, чем первой.
- 4. Преодоление дистанция с резко переменной скоростью.
Большинство авторов считают, что наиболее рациональным вариантом распределения усилий в индивидуальной гонка преследования на 4 км является относительно равномерное поддержание скорости на всей дистанции (1-й тип). Критерием оптимальности тактики при этом, как правило, выбирается сам спортивный результат (Т — →min) и реже среднее линейное отклонение скорости на отдельных участках дистанции от среднедистанционной скорости в гонке
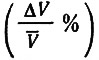
Некоторые авторы, например Ю. К. Дравниек (1977—1981) и М. А. Андрюнин с соавт. (1981) основным критерием оптимальности тактики считают показатель энергетической стоимости выполненной работы. Ими было определено, что тактические варианты распределения сил индивидуально-оптимальны и зависят от энергетического потенциала спортсмена.
Итак, на сегодняшний день у специалистов по велосипедному спорту нег единого мнения по вопросу выбора оптимальной тактики в индивидуальной гонке преследования на 4 км. В связи с этим целью нашего исследования явилось изучение закономерностей тактики в условиях соревновательной деятельности гонщиков-преследователей.
Для этого в работе были поставлены следующие задачи:
1. Определить тактические варианты прохождения дистанции индивидуальной гонки преследования на 4 км спортсменами высокой квалификации.
2. Выявить особенности тактики прохождения дистанции 4 км в зависимости от типа заезда.
Методика и организация исследования
Вся работа была проведена на олимпийском велотреке в Крылатском, позволяющем более качественно изучить тактическую деятельность велосипедистов, поскольку на варианты распределения усилий в гонке не оказывают влияния метеоусловия и другие факторы, имеющие место на открытых треках.
Было проанализировано более 150 графиков прохождения дистанции индивидуальной гонки преследования на 4 км сильнейшими гонщиками СССР и мира за период с 1980 по 1983 г. На первом этапе работы было рассмотрено 80 графиков предварительных заездов, в которых спортсмены отбираются в числе 16 или 8 участников, продолжающих борьбу в соревнованиях. По мнению ряда авторов (В. А. Бахвалов, 1960; А. А. Красников, 1968, Ю. Г. Крылатых, 1980 и др.), именно в заездах на время велосипедисты стремятся пройти дистанцию с оптимальной скоростью, а вариант распределения усилий на дистанции отражает уровень их специальной подготовленности.
На втором этапе работы исследовалась динамика скорости преодоления дистанции 4 км в финальных заездах.
Результаты исследования
Анализ графиков прохождения гонщиками дистанции в индивидуальной гонке преследования на 4 км показал, что на различных участках дистанции изменяется:
- стартовый набор скорости,
- падение скорости до уровня ниже среднедистанционной,
- поддержание скорости,
- увеличение скорости на финише.
Однако информация, полученная при регистрации и анализе динамики соревновательной скорости, сама со себе не позволяет решить вопрос о причинах изменения скорости на дистанции. Иными словами, не ясно, приводит ли увеличение скорости на предыдущем участке дистанции к вынужденному снижению скорости на последующем, более ясную картину дает корреляционный анализ связей между величинами скорости на отдельных километрах дистанции гонки. Заметим, что использовать корреляционный анализ можно лишь в том случае, если результаты измерения подчиняются закону нормального распределения.
Поэтому был построен график эмпирического закона распределения средней скорости в исследуемых заездах (рис. 1). В результате было установлено, что средние величины скорости велосипедистов подчиняются нормальному закону распределения. Поэтому для вычисления коэффициентов корреляции можно использовать формулу Бравэ-Пирсона (табл. 1).

Из табл. 1 видно, что средняя скорость первого километра дистанции имеет незначительную связь со вторым километром и практически не оказывает влияния на третий и четвертый километры дистанции. А поддержание высокой скорости на втором километре положительно влияет на результат прохождения третьего километра дистанции (rtk=0,766). Способность удерживать высокую скорость на третьем километре дистанции положительно влияет на время преодоления четвертого километра (rtk=0,674). Следовательно, на среднюю скорость преодоления последующего участка дистанции оказывает влияние скорость, показанная на предыдущем участке.
Статистические методы исследования позволили не только выявить влияние скорости прохождения одного участка дистанции на другой, но и определить значимость времени прохождения каждого участка дистанции на конечный результат. Для этого мы определили коэффициент корреляции между средней скоростью, показанной в гонке, и скоростью, зафиксированной на отдельных участках дистанции (рис. 2). Как видно, скорость на первых трех кругах имеет невысокую корреляционную связь с результатом в гонке (rtk=0,212—0,433). Средняя скорость, показанная с четвертого по одиннадцатый круги, имеет наибольшую корреляционную связь с результатом (rtk=0,613—0,844). Скорость на последних двух кругах имеет корреляционную связь с результатом на уровне rtk=0,251—0,655. Полученные данные свидетельствуют, что на результат в индивидуальной гонке преследования на 4 км оказывает влияние в основном способность гонщиков поддерживать высокую скорость в середине дистанции. Начало дистанции и финишное ускорение не являются определяющими в общем результате, поскольку выполняются всеми гонщиками с различной скоростью.
С этих позиций мы и подошли к изучению тактики в индивидуальной гонке преследования на 4 км у спортсменов высокой квалификации. В зависимости от динамики стартового ускорения, динамики скорости в середине и конце дистанции все исследуемые графики прохождения дистанции были разделены на 9 групп, представляющих различные варианты распределения усилий (табл. 2).

Поскольку ранее ни одна из классификаций динамики соревновательной скорости в гонке на 4 км не имела такого количества исследуемых тактических вариантов раскладок, мы предприняли попытку описать и охарактеризовать каждый из них.
1. Динамика дистанционной скорости носит переменный характер. После выполнения стартового ускорения и снижения скорости до уровня среднедистанционной наблюдается увеличение скорости в середине дистанции и ка финише при максимальном повышении скорости на старте +6,019% и снижении ее до —2,614%.
2. Скорость в начале дистанции превышает среднедистанционную на +9,495%, затем снижается (—1,726%) и остается практически неизменной до финиша.
3. Повышение скорости связано с выполнением сильного стартового ускорения, превышающего на 6,688% среднедистанционную скорость. В дальнейшем наблюдается снижение скорости сначала до уровня среднедистанционной, а затем и ниже среднедистанционной при максимальном снижении на —3,881% и некотором увеличении при финишном ускорении.
4. Разновидность третьего варианта при еще более сильном повышении скорости в начале дистанции (+7,624%) и характерном удержании скорости после каждого ее снижения. Максимальное снижение скорости составляет —3,972% от среднедистакционной.
5. Отмечается относительно равномерное прохождение дистанции. Максимальное повышение среднедистанционной скорости на старте составило +3,278%, а максимальное снижение в конце дистанции —2,355%.
6. Повышается среднедкстанционная скорость в начале и в конце дистанции и удерживается практически на одном уровне ниже среднедистанционной, в середине гонки. Максимальное повышение среднедистанционной скорости на старте составляет +5,736%.
7. Разновидность пятого варианта при значительном повышении среднедистанционной скорости на старте (+7,799%) и более раннем снижении скорости к финишу. Максимальное снижение среднедистанционной скорости составляет —4,939%.
8. Постепенное снижение скорости до финиша после выполнения стартового ускорения. Максимальное повышение среднедистанционной скорости составляет +10,125%, а минимальное снижение —6,349%.
9. После стартового ускорения скорость в гонке постепенно снижается практически на всей дистанции, за исключением короткого финишного отрезка, где скорость увеличивается. Максимальное повышение скорости составляет +8,988%, максимальное снижение —6,047% от среднедистанционной.
Рассчитанный коэффициент корреляции (rtk) меж_ду среднедистанционной скоростью в гонке (V) и величиной среднего линейного отклонения скорости на отдельных участках дистанции
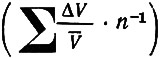
равен —0,790%, при P<0,1. Это свидетельствует, что высококвалифицированные велосипедисты стремятся к более равномерному поддержанию скорости на дистанции гонки. Явление это не случайное, а закономерное и зависит от индивидуальных возможностей организма спортсмена. Полученные данные по характеру динамики скорости в гонке согласуются с проведенными ранее лабораторными исследованиями при моделировании соревновательной деятельности на велоэргометре (А. И. Головачев, Ю. Г. Крылатых, 1981).
Чаще всего использовались варианты III, IV и VII, при которых среднедистанционная скорость наблюдалась в диапазоне 13,577—-13,842 м/с (см. табл. 2). Победители соревнований в основном применяли I и III тактические варианты, а аутсайдеры — V, VI, VIII и IX варианты.
Дальнейшее исследование тактики прохождения дистанции в индивидуальной гонке преследования на 4 км выявило, что на динамику скорости не всегда оказывают влияние действия соперника в заезде. Так, в различных по типу заездах было отмечено, что сильнейшие спортсмены мира стремятся придерживаться одного тактического варианта (рис. 3). Например, спортсмен из команды ГДР X. Вольф, занявший 4-е место на XXII Олимпийских играх, в предварительном, четвертьфинальном и полуфинальном заездах (см. рис. 3, а) преодолевал дистанцию, используя по предложенной нами классификации VIII тактический вариант. При этом в предварительном заезде, когда спортсмены стартовали по одному, X. Вольф установил новый мировой рекорд (4.39,96) для закрытых велотреков. В финальном заезде X. Вольф использовал VI тактический вариант, начав гонку медленнее, чем обычно на —2,25%. Относительно равномерно прошел 2-й и 3-й км дистанции и увеличил скорость на финише на +1,66% относительно среднеднстанционной. В этом заезде гонщик из ГДР показал один из лучших своих результатов (4.37,38), однако этого было недостаточно для победы над Х.-Х. Орстедом, занявшим 3-е место, — 4.36,54.
Чемпион Олимпийских игр 1980 года Р. Дилл-Бунди использовал в своих заездах VI тактический вариант (см. рис. 3, б). Учитывая свои скоростные возможности, швейцарский велосипедист начал гонку с высокой скоростью, превышая среднедистанционную более чем на 2—3%. Затем, после падения скорости на 1—2% ниже среднедистанционной, удерживал ее до девятого круга. В заключительной части дистанции, как правило, значительно увеличивал скорость (финишное ускорение), что позволило ему в финальном заезде на 8% превысить среднедистанционную скорость. Следует отметить, что при таком варианте распределения сил в гонке Р. Дилл-Бунди показал абсолютно лучшее время прохождения 4-километровой дистанции (4.32,29).
Таким образом, высокий спортивный результат в индивидуальной гонке преследования на 4 км может быть показан практически при любом варианте распределения усилий в гонке. Это еще раз подтвердило наше экспериментальное исследование в лабораторных условиях (М. А. Андрюнин с соавт., 1981), показавшее целесообразность использования понятия индивидуально-оптимального варианта распределения сил в гонке, позволяющего полностью исчерпать энергетический потенциал, зависящий от специальной подготовленности спортсменов. Поэтому мы считаем, что для каждого спортсмена существует свой индивидуально-оптимальный тактический вариант.
Отметим, что проводимое нами наблюдение за использованием вариантов распределения усилий в гонке сильнейшими велосипедистами СССР, выявило сохранение индивидуальных особенностей показателей тактики. Так, например, у неоднократного чемпиона СССР змс А. Краснова характер распределения усилий в гонках на протяжении 1980—1981 гг. (рис. 4) носил идентичный характер. Спортсмен использовал III тактический вариант. После превышения среднедистанционной скорости на 6— 8% во время стартового ускорения следовало снижение скорости до 5-го круга. Затем спортсмен удерживал скорость, близкую к среднедистанционной. Лучше всего А. Краснову удалось это сделать на зимнем первенстве СССР (27.01,81), где он показал высокий спортивный результат — 4.36,10.
Таким образом, мы пришли к выводу, что у велосипедистов высокой квалификации характер распределения усилий в гонке (динамика скорости) индивидуально-оптимален и сохраняется не только в зависимости от типа заезда, но и практически не изменяется на протяжении длительного времени участия в соревнованиях.
А. И. Головачев, ВНИИФК, Ю. Г. Крылатых, кандидат педагогических наук, ГЦОЛИФК.
Велосипедный спорт. Ежегодник. 1984 год.
Предыдущие статьи
→ О технике педалирования велосипедистов-шоссейников
→ Индивидуальность и оптимальность вариантов ведения гонки
→ Эффективность работы спортсмена при гонке преследования на 4 км
→ Измерение факторов для оценки скоростно-силовой подготовленности
→ Влияние тренировочных нагрузок на равнине и в горах
→ Факторы влияющие на силу воздушного сопротивления в велоспорте
→ Тенденции двухциклового планирования подготовки велосипедистов
→ Тренировка шоссейников при различном объеме нагрузки
→ Оценка качества педалирования велосипедиста
→ Особенности подготовки к заездам на сверхдлинные дистанции
→ Индивидуальность и оптимальность вариантов ведения гонки
→ Эффективность работы спортсмена при гонке преследования на 4 км
→ Измерение факторов для оценки скоростно-силовой подготовленности
→ Влияние тренировочных нагрузок на равнине и в горах
→ Факторы влияющие на силу воздушного сопротивления в велоспорте
→ Тенденции двухциклового планирования подготовки велосипедистов
→ Тренировка шоссейников при различном объеме нагрузки
→ Оценка качества педалирования велосипедиста
→ Особенности подготовки к заездам на сверхдлинные дистанции
Текущая статья
• Анализ тактики в индивидуальной гонке преследования на 4 км
Разместите ссылку на статью на своем сайте, блоге или форуме:
HTMLTextBB Code
Напишите свой отзыв к этой статье
Пока нет комментариев, смелее!
Лутц Хесслих — чемпион в спринтерской гонке на 1 км 1980 года
Олег Чужда — чемпион мира в командной гонке на 100 км
Роберт Дилл-Бунди — чемпион гонки преследовании на 4 км 1980 года
Индивидуальность и оптимальность вариантов ведения гонки
Групповая шоссейная гонка среди женщин на чемпионате мира 1980 года
Итоги выступления советских велосипедистов в гонках по треку
Чемпионат мира в гонках по треку 1983 года в Цюрихе
Сергей Копылов — трехкратный чемпион мира в гонках на треке
Велопробег Мира-83 против гонки вооружений